Sprawdzian wiedzy o gospodarce – najważniejsze zagadnienia modułu ogólnego 3/5

Dylemat więźnia to jedno z najczęstszych zagadnień występujących na egzaminie wstępny na studia magisterskie SGH! W tym artykule dowiesz się jak rozwiązywać zadania związane z tym zagadnieniem!

Sprawdzian kwalifikacyjny na studia magisterskie na SGH (sprawdzian wiedzy o gospodarce) w roku akademickim 2021/2022 składać się będzie z trzech modułów:

językowo-ogólnego (język obcy, mikroekonomia, makroekonomia);
ilościowego (matematyka, ekonometria, statystyka);
jakościowego (zarządzanie i marketing, finanse, integracja europejska);

Każdy z kandydatów zobowiązany jest przystąpić do części ogólnej oraz jednej z dwóch pozostałych – w zależności od kierunku, na który się rekrutuje.

Sprawdzian wiedzy o gospodarce co roku prezentuje wysoki poziom trudności, stanowiąc skuteczne sito selekcji. Wśród pytań pojawiają się zarówno niuansowe zadania teoretyczne, jak i skomplikowane polecenia obliczeniowe. Żeby pomóc Wam odpowiednio przygotować się do nauki przygotowaliśmy serię artykułów, które stanowią opis najważniejszych zagadnień wchodzących w skład poszczególnych modułów. Cykl ten jest jednocześnie prezentacją przykładowych wykresów, obliczeń czy wyjaśnień, które wchodzą w skład pełnego kursu przygotowującego do egzaminu wstępnego.

Dokładny opis kursu znajdziesz w dedykowanej zakładce na stronie internetowej.

Dylemat więźnia – teoria

Dylemat więźnia to najbardziej znana gra w ramach teorii gier. Stanowi ona uniwersalny schemat podejmowania decyzji przez co najmniej dwóch graczy, którzy mają przynajmniej dwie strategie możliwe do wyboru i działają w warunkach asymetrii informacji. Omówimy to zagadnienie na następującym przykładzie:

Fred i Bob zostali aresztowani za posiadanie nielegalnej broni. Wcześniej dokonali razem napadu na bank, ale prokurator ma niewystarczające dowody i może ich skazać za to przestępstwo jedynie, jeśli jedno z nich się przyzna. Oboje przestępcy są przetrzymywani w osobnych pokojach przesłuchań i w żaden sposób nie mogą się ze sobą kontaktować. Podczas odrębnych przesłuchań więźniom mówi się, że:

jeśli żadne z nich się nie przyzna, wówczas oboje zostaną skazani na 2 lata więzienia za nielegalne posiadanie broni,
jeśli jedno z nich się przyzna, a drugie nie, wówczas to, które się przyzna zostanie ułaskawione, a drugie zostanie skazane na 10 lat więzienia za napad na bank,
jeśli oboje się przyznają, wówczas oboje zostaną skazani na 4 lata więzienia.

Sposób rozumowania Boba: Nie wiem co zamierza zrobić Fred. Jeśli będzie milczał, najlepszą strategią dla mnie jest przyznać się, ponieważ wtedy mnie wypuszczą i nie spędzę w więzieniu 2 lat. Jeśli Fred powie prawdę i się przyzna, też powinienem się przyznać, bo spędzę w więzieniu 4 lata zamiast 10. Zatem niezależnie co powie Fred, bardziej opłaca mi się powiedzieć prawdę.

Sposób rozumowania Freda będzie taki sam.

Równowaga Nasha, czyli „rozwiązanie” tej konkretnej gry, zostaje osiągnięta, gdy obaj więźniowie się przyznają, co wcale nie oznacza dla nich uzyskania najkorzystniejszego wyroku. Jednak nie mając pewności, co zrobi drugi więzień, decyzja o przyznaniu się była jak najbardziej racjonalna.

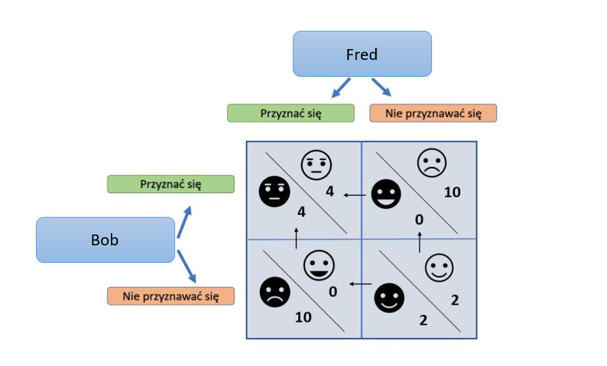
Każdy z nich spędzi w więzieniu po 4 lata, mimo że kooperując i obaj wstrzymując się od zeznawania mogliby skrócić wyrok do dwóch lat. To rozwiązanie (zwane optymalnym) nie ostanie jednak osiągnięte przez obawę, że drugi z graczy przyzna się i skaże pierwszego na dekadę odsiadki.

Dylemat więźnia – przykładowe zadanie

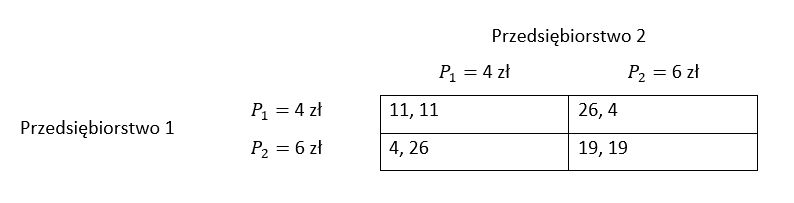
Dwa przedsiębiorstwa funkcjonują bez kooperacji, a decyzje dotyczące poziomu ceny sprzedawanego produktu (P1 = 4 zł lub P2 = 6 zł) podejmują jednocześnie. Macierz zysków jest przedstawiona poniżej. Pierwsza z wartości jest poziomem zysku przedsiębiorstwa 1, druga – przedsiębiorstwa 2. Wskaż prawdziwe stwierdzenie.

strategią dominującą dla obu z przedsiębiorstw jest P1; będzie równowaga Nasha
strategią dominującą przedsiębiorstwa 1. jest P1, a drugiego P2
strategią dominującą dla obu przedsiębiorstw jest P2; będzie równowaga Nasha
strategią dominującą przedsiębiorstwa 1. jest P2, a drugiego P1

Rozwiązanie:

Każdy z graczy wybiera strategię w oparciu o spodziewane zachowanie drugiego z graczy. Analizując macierz wypłat z perspektywy przedsiębiorstwa 1:

Jeżeli przedsiębiorstwo 2 wybierze P = 4 to przedsiębiorstwu 1 również opłaca się ustalić cenę na poziomie równym 4, ponieważ jego zyski wynoszą wtedy 11 zamiast 4 (lewa górna komórka tabeli zamiast prawej górnej),
Jeżeli przedsiębiorstwo 2 wybierze P = 6 to przedsiębiorstwu 1 opłaca się ustalić cenę na poziomie 4, ponieważ jego zyski wynoszą wtedy 26 zamiast 19 (prawa górna komórka tabeli zamiast prawej dolnej).

Oznacza to, że niezależnie od wyboru przedsiębiorstwa 2, przedsiębiorstwu 1 zawsze bardziej opłaca się wybrać cenę równą 4. Identycznie sytuacja będzie wygląda z punktu widzenia przedsiębiorstwa 2, ono również zawsze wybierze strategię niższej ceny. Mamy tutaj zatem do czynienia z kombinacją dwóch strategii dominujących. Jest to klasyczny przypadek dylematu więźnia, gdzie równowaga Nasha będąca na przecięciu strategii dominujących, czyli wypłaty (11; 11), nie jest optymalna dla graczy (19; 19)

Podsumowanie

Mamy nadzieję, że po lekturze tego tekstu ewentualne zadania oparte na zagadnieniu dylematu więźnia nie będą sprawiać Wam problemów!

Jeżeli bylibyście zainteresowani pełnymi przygotowaniami do egzaminu – zgłoście się do nas!

Sprawdź także nasze inne artykuły o rekrutacji na studia magisterskie SGH:

Grupa odnośnie rekrutacji

Chcesz być ze wszystkim na bieżąco? Dołącz do studenckiej grupy dotyczącej rekrutacji:

Sprawdzian wiedzy o gospodarce – najważniejsze zagadnienia modułu ogólnego 3/5 – dylemat więźnia

Dylemat więźnia – teoria

Dylemat więźnia – przykładowe zadanie

Podsumowanie

Sprawdź także nasze inne artykuły o rekrutacji na studia magisterskie SGH:

Grupa odnośnie rekrutacji