Test SGH - przykładowe zadania obliczeniowe 1/3

W związku z waszym entuzjastycznym przyjęciem naszej poprzedniej serii artykułów, która ukazywała po jednym zagadnieniu w ramach każdego działu tematycznego egzaminu wstępnego na SGH, postanowiliśmy przygotować kolejny cykl, tym razem poświęcony zadaniom matematycznym (równania popytu i podaży).

Test z wiedzy o przedsiębiorczości, mimo że bazuje głównie na wiedzy teoretycznej, wymaga niekiedy uporania się z całkiem nietrywialnymi poleceniami liczeniowymi. Pierwszy tekst związany z tą tematyką poświęcimy działaniom związanym z operacjami na równaniach popytu i podaży.

Krótkie przypomnienie – czym jest popyt i podaż (równania popytu i podaży)

Popyt opisuje zainteresowanie konsumenta danym produktem w zależności od jego ceny. Zgodnie z prawem popytu, gdy cena rośnie, to klient kupuje danego dobra mniej. Natomiast kiedy cena maleje (np. na skutek rabatów), nabywa to dobro w większej ilości.

Możemy, wobec tego matematycznie nazwać popyt funkcją, która różnym poziomom ceny (P) przyporządkowuje odpowiadające im ilości zakupywanego dobra (Q). W postaci ogólnej funkcja ta przyjmuje następującą postać:

Test SGH zadania - Test z wiedzy o przedsiębiorczości - wzór 1

Zauważ, że jest to funkcja liniowa, w której:

b – to wyraz wolny;

a – współczynnik kierunkowy funkcji popytu, będący niemal zawsze liczbą ujemną.

Podaż z kolei określa skłonność producenta do wytwarzania dóbr i usług, również uzależnioną od ich ceny. Wobec tego prawo podaży mówi nam, że gdy produkt drożeje, to przedsiębiorca produkuje go w większej ilości, z kolei, gdy produkt na rynku jest tańszy, to w mniejszej.

Matematycznie funkcja podaży przyjmuje poniższą postać:

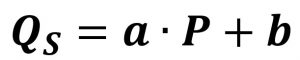
Test SGH zadania - Test z wiedzy o przedsiębiorczości - wzór 2

Jak łatwo zauważyć, jest ona podobna do funkcji popytu, z tą różnicą, że w funkcji podaży współczynnik kierunkowy jest zawsze liczbą dodatnią.

Funkcje te służą m.in. do określania równowagi rynkowej, czyli sytuacji, w której na rynku ustala się cena równoważąca wielkość popytu i podaży. Innymi słowy, producenci wytwarzają dokładnie tyle dóbr, ile chcą kupić nabywcy.

Przypomnieliśmy więc najważniejsze podstawy – czas przejść do kilku zadań, w których wykorzystamy powyższą wiedzę.

Zadanie 1 – podatek od produkcji

Treść zadania:

Rynkowa funkcja podaży pewnego rodzaju baterii dana jest wzorem Q=36+2P. Natomiast funkcja popytu Q=114-4P, gdzie Q – liczba baterii (w mln szt.), P – cena baterii (w zł). Pod naciskiem ekologów rząd wprowadza opłatę produktową pobieraną od producentów w wysokości 2 zł/szt. Ile będzie wynosić nowa cena i ilość równowagi?

Rozwiązanie:

Wprowadzenie opłaty produktowej pobieranej od producentów jest rodzajem podatku od ilości. Niezależnie od tego, na jakim poziomie znajdzie się teraz cena (można domyślać się, że przedsiębiorcy przynajmniej odrobinę ją podniosą, by zrekompensować sobie konieczność oprowadzania podatku), od dowolnego jej poziomu firma otrzymuje tylko to, co zostanie po odprowadzeniu 2 zł daniny państwowej. Nowa funkcja podaży będzie miała zatem postać:

Q = 36 + 2(P – 2)

Równanie funkcji popytu nie ulega zmianie, ponieważ nie zmieniła się żadna z determinant działania konsumentów.

Wobec tego równowagę rynkową wyznaczamy poprzez przyrównanie „nowej” funkcji podaży oraz dotychczasowej funkcji popytu:

36 + 2(P-2) = 114 – 4P

W wyniku otrzymujemy:

P = 13,67 zł

Q = 59,33 mln szt.

Zadanie 2 – subsydium produkcyjne

Zamiast treści zadania:

Polecenia związane z subsydium produkcyjnym, czyli, innymi słowy, dopłatą do produkcji otrzymywaną przez przedsiębiorstwa od państwa, wymagają bardzo podobnych obliczeń jak te związane z podatkiem. Załóżmy, że dla danych z poprzedniego zadania jedyna zmiana to wprowadzenie subwencji 2 zł (zamiast podatku) dla każdej produkowanej sztuki.

Jak teraz będzie wyglądała funkcja podaży?

Q = 36 + 2(P + 2)

Możesz, wobec tego zapamiętać, że jeśli:
t – to nominalna wartość podatku (od ang. tax);

s – nominalna wartość subsydium (od ang. subsidy);

To przy ogólnej postaci funkcji podaży:

Zadania na podatek wymagają jej przekształcenia do postaci:

Natomiast zadania na subsydium:

Resztę rozwiązania zadania drugiego zostawiamy do twojej samodzielnej pracy!

Zadanie 3 – wyznaczanie równania podaży

Treść zadania:

Wiedząc, że cena równowagi wynosi 300 zł, ilość równowagi rynkowej 150 szt., a współczynnik kierunkowy funkcji podaży 1,5, wyznacz równanie funkcji podaży tego przedsiębiorstwa.

Rozwiązanie:

Przypomnijmy sobie ogólną postać funkcji podaży:

Po podstawieniu danych z treści zadania otrzymujemy ją w postaci:

150 = 1,5 * 300 + b

Wobec tego współczynnik kierunkowy funkcji wynosi:

b = 150 – 1,5 * 300 = -300

Zatem równanie podaży ma postać:

Równania popytu i podaży – podsumowanie

Jak sami widzicie – zadania na egzaminie wstępnym potrafią zaskoczyć. Osoby przekonane, że otrzymają wysokie wyniki bez umiejętności rozwiązywania zadań matematycznych, są w dużym błędzie! Jeśli chcesz kompleksowo przygotować się na wszystkie niespodzianki, jakie możesz napotkać na teście z wiedzy o przedsiębiorczości, to już dziś zapisz się na najbardziej skuteczne w Polsce kursy EduFactory!

Chcesz dowiedzieć się, czego jeszcze możesz spodziewać się na teście, poza zagadnieniem “równania popytu i podaży”?

Sprawdź – napisaliśmy o tym na naszym blogu:

Grupa odnośnie rekrutacji

Chcesz być ze wszystkim na bieżąco? Dołącz do studenckiej grupy dotyczącej rekrutacji:

Test z wiedzy o przedsiębiorczości – zadania obliczeniowe 1/3 – równania popytu i podaży